Decentralized Multi-Robot Coordination via Task Allocation
We are interested in scalable approaches for multi-robot coordination. One fundamental framework to achieve this goal is the decentralized or distributed task allocation. There are several open challenges that complicate designing—especially analyzing—decentralized algorithms. For example, the information attained by individual robots may be incomplete and inaccurate, resources can be limited, communication can be constrained, and action decisions may have to be conservative due to sub-optimal or uncertain results. Within the distributed context, I have been particularly interested in improving performance in terms of computation and communication complexities, solution quality, robustness, hierarchical flexibility, etc.
Task Allocation Uncertainty Assessment
We have developed an extremely fast sensitivity analysis method for classic assignment problem (O(n^2) time for each variable). It is achieved through modifying the matching graph operations of the well-known Hungarian algorithm, so that the standard computation is relaxed and bounds are produced. Different from existing uncertainty analysis approaches most of which utilize the stochastic means, this algorithm is a deterministic method with bounded time complexity.
iRobots with particle-filter SLAM used to analyze sensitivity of task allocation.
The robots we used are the create type made by iRobot, as shown right figure. A Hokuyo laser range sensor is mounted on each robot which records range data up to ∼5 m and an ASUS netbook is carried by each robot to compute all data including the communication, utility estimation, interval analysis, logging, etc.
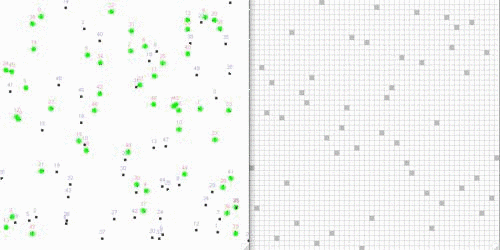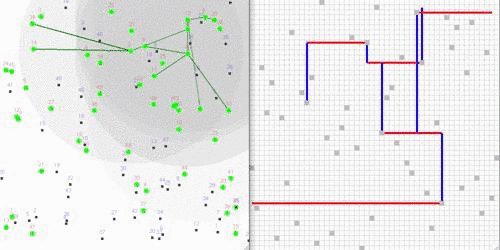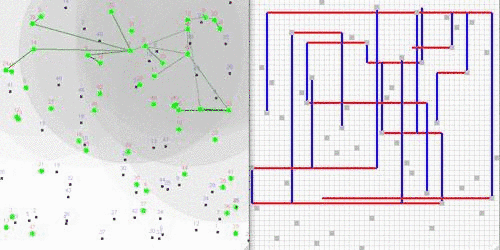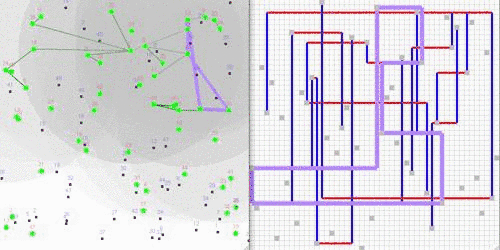
Task-Swap-based Anytime Algorithm:
I developed a fully decentralized task allocation approach that allows local search processes to execute concurrently while minimizing interactions amongst the processes, needing neither global broadcast nor a multi-hop communication protocol. The formulation is analyzed in a novel way using tools from group theory and optimization duality theory to show that the convergence of local searching processes is related to a shortest path routing problem on a graph subject to the network topology.
Optimal Market-based Method:
Rather than adopting a buyer's "selfish" bidding perspective as in existing auction/market-based approaches, we developed an auctioning mechanism from a merchant’s point of view, producing a pricing policy that responds to cliques of customers and their preferences. Our algorithm uses price escalation to clear a market of all its items, producing a state of equilibrium that satisfies both the merchant and customers.
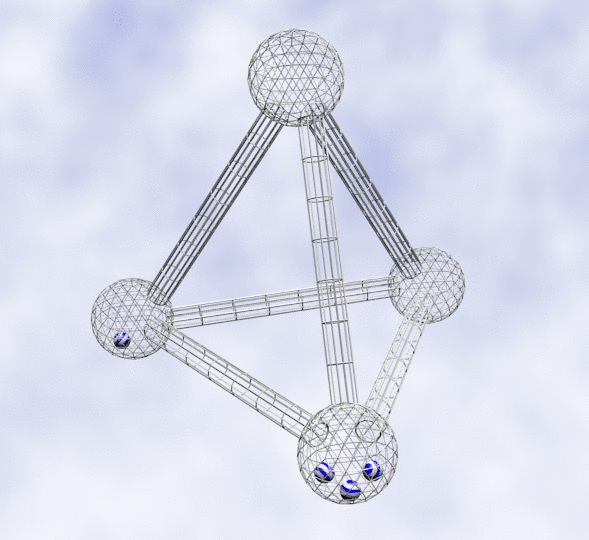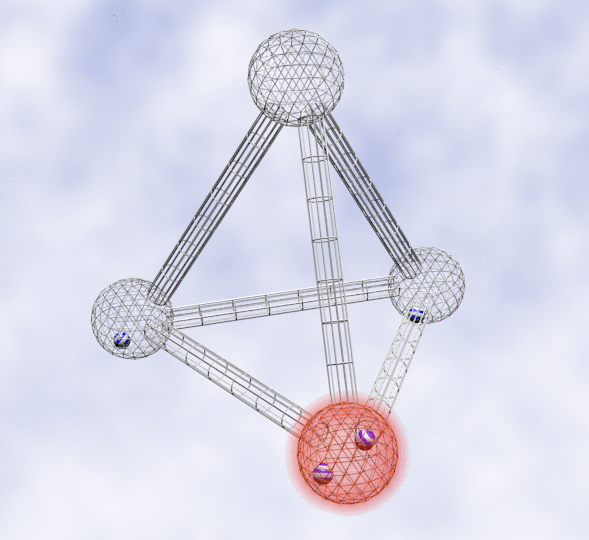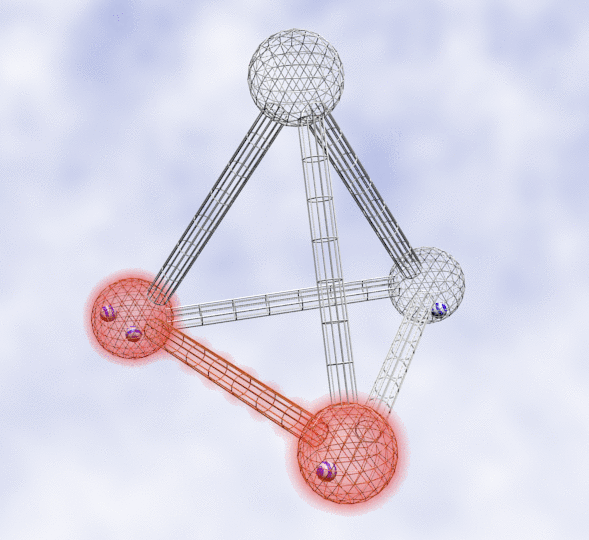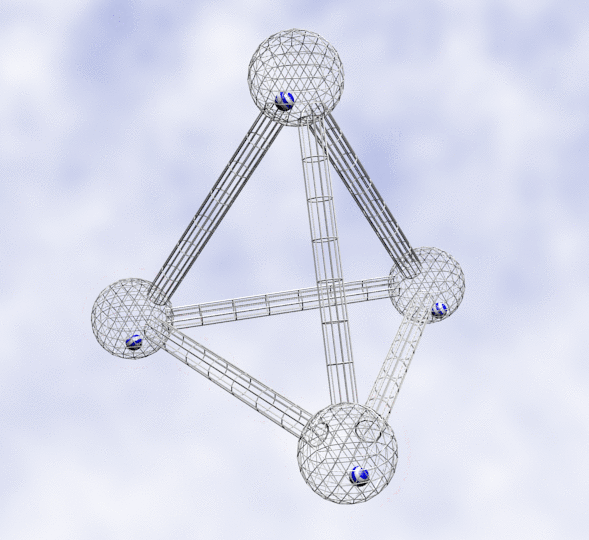
Right figure: Visualization as an equilibrium flow. We wish to manipulate the four striped balls so they flow into four wired spherical containers that are connected with tunnels among each other. The way to remove balls from a wired container is to create a perturbation, i.e., add energy to a container to make the enclosed balls unstable (imagine the balls behave like heated microscopic particles). The essence of the algorithm is that it always adds the minimum energy required to push exactly one ball out of a crowded container; and it guarantees that a ball will never flow back into an already heated sphere.
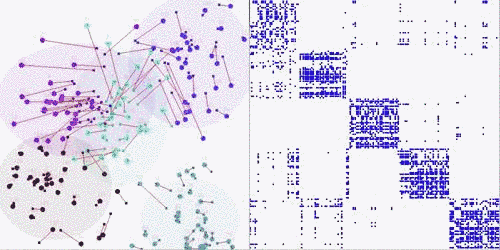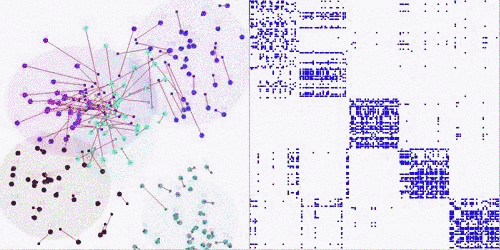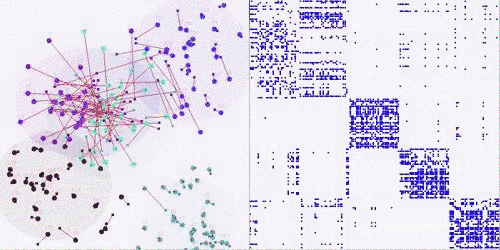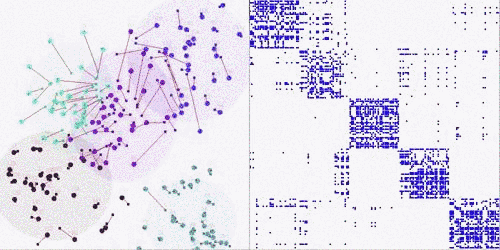
Matrix Coarsening and Partition:
We observe that an assignment can be computed through coarsening and partitioning operations on the standard utility matrix via a set of mature partitioning techniques and programs. We designed an adaptive algorithm that mixes centralized and decentralized approaches dynamically at different scales to produce a fast, robust method that is accurate and scalable, and reduces both the global communication and unnecessary repeated computation.


